Глава 12. Рекурсия
Понятие рекурсии
Рекурсивным
называется объект, частично состоящий или определяемый с помощью самого себя.
Факториал — это классический пример рекурсивного объекта. Факториал числа п —
это произведение целых чисел от 1 до п. Обозначается факториал числа п так:
n!.
Согласно
определению
n! = 1
х 2 х 3 х ... х (п - 1) х п. Приведенное выражение можно
переписать так:
n! = nх ((n - 1) х (n - 2)
х ...х 3 х 2 х 1) = n х (n - 1)!
То есть,
факториал числа п равен произведению числа п на факториал числа (п - 1). В свою
очередь, факториал числа («-!) — это произведение числа (п - 1) на факториал
числа (п - 2) и т. д.
Таким образом,
если вычисление факториала п реализовать как функцию, то в теле этой функции
будет инструкция вызова функции вычисления факториала числа (п - 1), т. е.
функция будет вызывать сама себя. Такой способ вызова называется рекурсией, а
функция, которая обращается сама к себе, называется рекурсивной
функцией.
В листинге 12.1
приведена рекурсивная функция вычисления факториала.
Листинг
12.1. Рекурсивная функция вычисления факториала
function factorial(n: integer): integer;
begin
if n <>
1
then factorials n * factorial(n-1)
// функция вызывает сама себя
else factorial := 1; // рекурсивный процесс закончен
end;
Обратите
внимание, что функция вызывает сама себя только в том случае, если значение
полученного параметра k не равно единице. Если значение параметра равно единице,
то функция сама себя не вызывает, а возвращает значение, и рекурсивный процесс
завершается.
На рис. 12.1
приведен вид диалогового окна программы, которая для вычисления факториала числа
использует рекурсивную функцию factorial. Текст программы приведен в листинге
12.2.
Рис. 12.1.
Окно программы вычисления факториала
Листинг
12.2. Использование рекурсивной функции
unit factor
;
interface
uses
Windows, Messages, SysUtils, Classes,
Graphics, Controls, Forms,
Dialogs, StdCtrls;
type
TForm1 =
class(TForm)
Label1:
TLabel;
Edit1:
TEdit;
Button1:
TButton;
Label2:
TLabel;
procedure ButtonlClick(Sender: TObject) ;
private
{ Private declarations }
public
{ Public declarations }
end;
var
Form1:
TForm1;
implementation
{$R *.DFM}
// рекурсивная
функция
function
factorial(n: integer): integer;
begin
if n >
1
then factorial := n
* factorial(n-1) // функция вызывает сама себя
else factorial:= 1; // факториал 1 равен 1
end;
procedure TForml.ButtonlClick(Sender: TObject);
var
k:integer; // число,
факториал которого надо вычислить
f:integer; // значение факториала числа k
begin
k :=
StrToInt(Edit1.Text);
f :=
factorial(k);
label2.caption:='Факториал
числа '+Edit1.Text
+ ' равен '+IntToStr(f);
end;
end.
На рис. 12.2
приведены два диалоговых окна. Результат вычисления факториала, представленный
на рис. 12.2, а, соответствует ожидаемому.
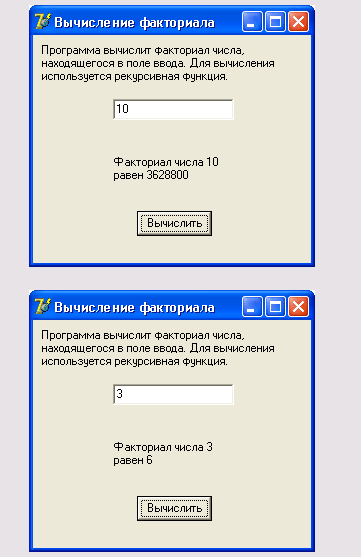
Рис. 12.2.
Примеры работы программы вычисления факториала
Результат,
представленный на рис. 12.2, б, не соответствует ожидаемому. Факториал числа 44
равен нулю! Произошло это потому, что факториал числа 44 настолько велик, что
превысил максимальное значение для переменной типа integer, и, как говорят
программисты, произошло переполнение с потерей значения.
Delphi может
включить в исполняемую программу инструкции контроля диапазона значений
переменных. Чтобы инструкции контроля были добавлены в программу, нужно во
вкладке Compiler диалогового окна Project Options (рис. 12.3)
установить флажок Overflow checking (Контроль переполнения), который
находится в группе Runtime errors (Ошибки времени
выполнения).

Рис. 12.3. Вкладка Compiler диалогового окна Project Options